Вычислить определитель матрицы онлайн. Вычисление определителя матрицы онлайн Способы разложения определителя

Понятие определителя n -го порядка

Пользуясь этой статьёй об определителях, вы обязательно научитесь решать задачи вроде следующей:

Решить уравнение:

и многих других, которые так любят придумывать преподаватели.

Определитель матрицы или просто определитель играет важную роль в решении систем линейных уравнений. В общем-то определители и были придуманы для этой цели. Поскольку часто говорят также "определитель матрицы", упомянем здесь и матрицы. Матрица - это прямоугольная таблица, составленная из чисел, которые нельзя менять местами. Квадратная матрица - таблица, у которой число строк и число столбцов одинаково. Определитель может быть только у квадратной матрицы .

Понять логику записи определителей легко по следующей схеме. Возьмём знакомую вам со школьной скамьи систему из двух уравнений с двумя неизвестными:

В определителе последовательно записываются коэффициенты при неизвестных: в первой строке - из первого уравнения, во второй строке - из второго уравнения:

Например, если дана система уравнений

то из коэффициентов при неизвестных формируется следующий определитель:

Итак, пусть дана квадратная таблица, состоящая из чисел, расположенных в n строках (горизонтальных рядах) и в n столбцах (вертикальных рядах). С помощью этих чисел по некоторым правилам, которые мы изучим ниже, находят число, которое и называют определителем n -го порядка и обозначают следующим образом:

(1)

Числа называют элементами определителя (1) (первый индекс означает номер строки, второй – номер столбца, на пересечении которых стоит элемент; i = 1, 2, ..., n; j = 1, 2, ..., n). Порядок определителя – это число его строк и столбцов.

Воображаемая прямая, соединяющая элементы определителя, у которых оба индекса одинаковы, т.е. элементы

называется главной диагональю , другая диагональ – побочной .

Вычисление определителей второго и третьего порядков

Покажем, как вычисляются определители первых трёх порядков.

Определитель первого порядка – это сам элемент т.е.

Определитель второго порядка есть число, получаемое следующим образом:

, (2)

Произведение элементов, стоящих соответственно на главной и на побочной диагоналях.

Равенство (2) показывает, что со своим знаком берётся произведение элементов главной диагонали, а с противоположным – произведение элементов побочной диагонали .

Пример 1. Вычислить определители второго порядка:

Решение. По формуле (2) находим:

Определитель третьего порядка – это число, получаемое так:

(3)

Запомнить эту формулу трудно. Однако существует простое правило, называемое правилом треугольников , которое позволяет легко воспроизвести выражение (3). Обозначая элементы определителя точками, соединим отрезками прямой те из них, которые дают произведения элементов определителя (рис. 1).

Формула (3) показывает, что со своими знаками берутся произведения элементов главной диагонали, а также элементов, расположенных в вершинах двух треугольников, основания которых ей параллельны; с противоположными – произведения элементов побочной диагонали, а также элементов, расположенных в вершинах двух треугольников, которые ей параллельны .

На рис.1 главная диагональ и соответствующие ей основания треугольников и побочная диагональ и соответствующие ей основания треугольников выделены красным цветом.

При вычислении определителей очень важно, как и в средней школе, помнить, что число со знаком минус, умноженное на число со знаком минус, в результате даёт число со знаком плюс, а число со знаком плюс, умноженное на число со знаком минус, в результате даёт число со знаком минус.

Пример 2. Вычислить определитель третьего порядка:

Решение. Пользуясь правилом треугольников, получим

Вычисление определителей n -го порядка

Разложение определителя по строке или столбцу

Для вычисления определителя n -го порядка необходимо знать и использовать следующую теорему.

Теорема Лапласа. Определитель равен сумме произведений элементов какой-либо строки на их алгебраические дополнения, т.е.

Определение . Если в определителе n -го порядка выбрать произвольно p строк и p столбцов (p < n ), то элементы, находящиеся на пересечении этих строк и столбцов, образуют матрицу порядка .

Определитель этой матрицы называется минором исходного определителя. Например, рассмотрим определитель :

Из строк и столбцов с чётными номерами построим матрицу:

Определитель

называется минором определителя . Получили минор второго порядка. Ясно, что из можно построить различные миноры первого, второго и третьего порядка.

Если взять элемент и вычеркнуть в определителе строку и столбец, на пересечении которых он стоит, то получим минор, называемый минором элемента , который обозначим через :

.

Если минор умножить на , где 3 + 2 – сумма номеров строки и столбца, на пересечении которых стоит элемент то полученное произведение называется алгебраическим дополнением элемента и обозначается ,

Вообще, минор элемента будем обозначать , а алгебраическое дополнение ,

(4)

Для примера вычислим алгебраические дополнения элементов и определителя третьего порядка :

По формуле (4) получим

При разложении определителя часто используется следующее свойство определителя n -го порядка:

если к элементам какой-либо строки или столбца прибавить произведение соответствующих элементов другой строки или столбца на постоянный множитель, то значение определителя не изменится.

Пример 4.

Предварительно вычтем из первой и третьей строк элементы четвёртой строки, тогда будем иметь

В четвёртом столбце полученного определителя три элемента – нули. Поэтому выгоднее разложить этот определитель по элементам четвёртого столбца, так как три первых произведения будут нулями. Поэтому

Проверить решение можно с помощью калькулятора определителей онлайн .

А в следующем примере показано, как вычисление определителя любого (в данном случае - четвёртого) порядка можно свести к вычислению определителя второго порядка.

Пример 5. Вычислить определитель:

Вычтем из третьей строки элементы первой строки, а к элементам четвёртой строки прибавим элементы первой строки, тогда будем иметь

В первом столбце все элементы, кроме первого, - нули. То есть, определитель можно уже разложить по первому столбцу. Но нам очень не хочется вычислять определитель третьего порядка. Поэтому произведём ещё преобразования: к элементам третьей строки прибавим элементы второй строки, умноженные на 2, а из элементов четвёртой строки вычтем элементы второй строки. В результате определитель, являющийся алгебраическим дополнением, сам может быть разложен по первому столбцу и нам останется только вычислить определитель второго порядка и не запутаться в знаках:

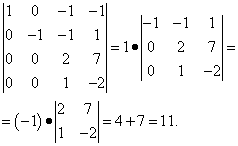
Приведение определителя к треугольному виду

Определитель, где все элементы, лежащие по одну сторону одной из диагоналей, равны нулю, называется треугольным. Случай побочной диагонали путём изменения порядка строк или столбцов на обратный сводится к случаю главной диагонали. Такой определитель равен произведению элементов главной диагонали.

Для приведения к треугольному виду используется то же самое свойство определителя n -го порядка, которое мы применяли в предыдущем параграфе: если к элементам какой-либо строки или столбца прибавить произведение соответствующих элементов другой строки или столбца на постоянный множитель, то значение определителя не изменится.

Проверить решение можно с помощью калькулятора определителей онлайн .

Свойства определителя n -го порядка

В двух предыдущих параграфах мы уже использовали одно из свойств определителя n -го порядка. В некоторых случаях для упрощения вычисления определителя можно пользоваться другими важнейшими свойствами определителя. Например, можно привести определитель к сумме двух определителей, из которых один или оба могут быть удобно разложены по какой-либо строке или столбцу. Случаев такого упрощения предостаточно и решать вопрос об использовании того или иного свойства определителя следует индивидуально.

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два» :

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 - нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Пример:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ . Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу :

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .

БУДЬТЕ ВНИМАТЕЛЬНЫ!

Дальнейшие свойства связаны с понятиями минора и алгебраического дополнения

Минором элемента называется определитель, составленный из элементов, оставшихся после вычеркивания стоки и столбца, на пересечении которых находится этот элемент. Минор элемента определителя порядка имеет порядок . Будем его обозначать через .

Пример 1. Пусть , тогда .

Этот минор получается из A путём вычёркивания второй строки и третьего столбца.

Алгебраическим дополнением элемента называется соответствующий минор, умноженный на , т.е , где –номер строки и -столбца, на пересечении которых находится данный элемент.

VІІІ. (Разложение определителя по элементам некоторой строки). Определитель равен сумме произведений элементов некоторой строки на соответствующие им алгебраические дополнения.

Пример 2. Пусть , тогда

Пример 3. Найдём определитель матрицы , разложив его по элементам первой строки.

Формально эта теорема и другие свойства определителей применимы пока только для определителей матриц не выше третьего порядка, поскольку другие определители мы не рассматривали. Следующее определение позволит распространить эти свойства на определители любого порядка.

Определителемматрицы порядка называется число, вычисленное с помощью последовательного применения теоремы о разложении и других свойств определителей.

Можно проверить, что результат вычислений не зависит от того, в какой последовательности и для каких строк и столбцов применяются вышеуказанные свойства. Определитель с помощью этого определения находится однозначно.

Хотя данное определение и не содержит явной формулы для нахождения определителя, оно позволяет находить его путём сведения к определителям матриц меньшего порядка. Такие определения называют рекуррентными.

Пример 4. Вычислить определитель:

Хотя теорему о разложении можно применять к любой строке или столбцу данной матрицы, меньше вычислений получится при разложении по столбцу, содержащему как можно больше нулей.

Поскольку у матрицы нет нулевых элементов, то получим их с помощью свойства VII . Умножим первую строку последовательно на числа и прибавим её ко строкам и получим:

Разложим получившийся определитель по первому столбцу и получим:

так как определитель содержит два пропорциональных столбца.

Некоторые виды матриц и их определители

Квадратная матрица, у которой ниже или выше главной диагонали стоят нулевые элементы ()называется треугольной.

Их схематичное строение соответственно имеет вид: или

.

Матрицы применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. При этом количество строк матрицы соответствует числу уравнений, а количество столбцов – количеству неизвестных. Как результат – решение систем линейных уравнений сводится к операциям над матрицами.

Матрица записывается в виде прямоугольной таблицы элементов кольца или поля (к примеру, целых, комплексных или действительных чисел). Является совокупностью строк и столбцов, на пересечении которых находятся ее элементы. Размер матрицы задается количеством строк и столбцов.

Важным значением любой матрицы является её определитель, который вычисляется по определённой формуле. Вручную необходимо проделать ряд операций с матрицей, чтобы вычислить её определитель. Определитель может быть как положительным, так отрицательным, так и равен нулю. Чтобы проверить свои вычисления определителя матрицы, Вы можете воспользоваться нашим онлайн калькулятором. Онлайн калькулятор мгновенно посчитает определитель матрицы и выдаст точное значение.

Определитель матрицы – это своеобразная характеристика матрицы, а точнее с помощью него можно определить имеет ли соответствующая система уравнений решение. Определитель матрицы широко используется в науке, такой как физика, с помощью которого вычисляется физический смысл многих величин.

Решение систем линейных алгебраических уравнений

Также с помощью нашего калькулятора вы сможете решить систему линейных алгебраических уравнений (СЛАУ).

Решение систем линейных алгебраических уравнений входит в число обычных задач линейной алгебры. СЛАУ и методы их решения лежат в основе многих прикладных направлений, в том числе в эконометрике и линейном программировании.

Бесплатный онлайн калькулятор

Наш бесплатный решатель позволит решить уравнение онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать - это просто ввести свои данные в калькуляторе. Так же вы можете посмотреть видео инструкцию и узнать, как решить уравнение на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей группе ВКонтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.

Определитель матрицы

Нахождение определителя матрицы является очень частой задачей в высшей математике и алгебре. Как правило, без значения определителя матрицы не обойтись при решении сложных систем уравнений. На вычислении определителя матрицы построен метод Крамера решения систем уравнений. С помощью определения детермината определяют наличие и единственность решения систем уравнений. Поэтому сложно переоценить важность умения правильно и точно находить определитель матрицы в математике. Методы решения определителей являются теоретически довольно простыми, однако с увеличением размера матрицы вычисления становятся очень громоздкими и требуют огромной внимательности и много времени. Очень легко в таких сложных математических вычислениях допустить незначительную ошибку или описку, что приведет к ошибке в окончательном ответе. Поэтому даже если вы находите определитель матрицы самостоятельно, важно проверить полученный результат. Это позволяет сделать наш сервис Нахождение определителя матрицы онлайн . Наш сервис выдает всегда абсолютно точный результат, не содержащий ни ошибок, ни описок. Вы можете отказаться от самостоятельных вычислений, поскольку с прикладной точки зрения, нахождение определителя матрицы не имеет обучающего характера, а просто требует много времени и числовых вычислений. Поэтому если в вашей задачи определение детерминанта матрицы являются вспомогательными, побочными вычислениями, воспользуйтесь нашим сервисом и найдите определитель матрицы онлайн !

Все вычисления проводятся автоматически с высочайшей точностью и абсолютно бесплатны. У нас очень удобный интерфейс для ввода матричных элементов. Но главное отличие нашего сервиса от аналогичных - возможность получения подробного решения. Наш сервис при вычислении определителя матрицы онлайн всегда использует самый простой и короткий метод и подробно описывает каждый шаг преобразований и упрощений. Так что вы получаете не просто значение детерминанта матрицы, окончательный результат, но и целое подробное решение.